向量叉积与点积的应用

前言

最近一直有用到向量的叉积与点积,所以在这里总结一下用法和心得。另外说明一下，这里的点积和叉积与数学上的还是有些区别的，因为数学上面是x,y,z。而我这里只涉及到了平面的x,y。不过方法是类似的,日后如果要做三维应该也是二维的推广。

点积

点积的概念: 一个向量在另一个向量上的投影的长度*另一个向量的长度,正负代表方向。

a(x1,y1),b(x2,y2) a,b向量的点积 = x1*x2+y1*y2。
点积代表的含义为向量a在b上的投影与b长度的乘积(反过来b在a上一样)

点积大于0的时候代表投影在另一个向量上，也就是说两个向量的角度差不超90

等于0的时候代表90度

小于零代表角度差大于90度

如下图所示,a向量与b向量的点积为正,与b`向量的点积为负。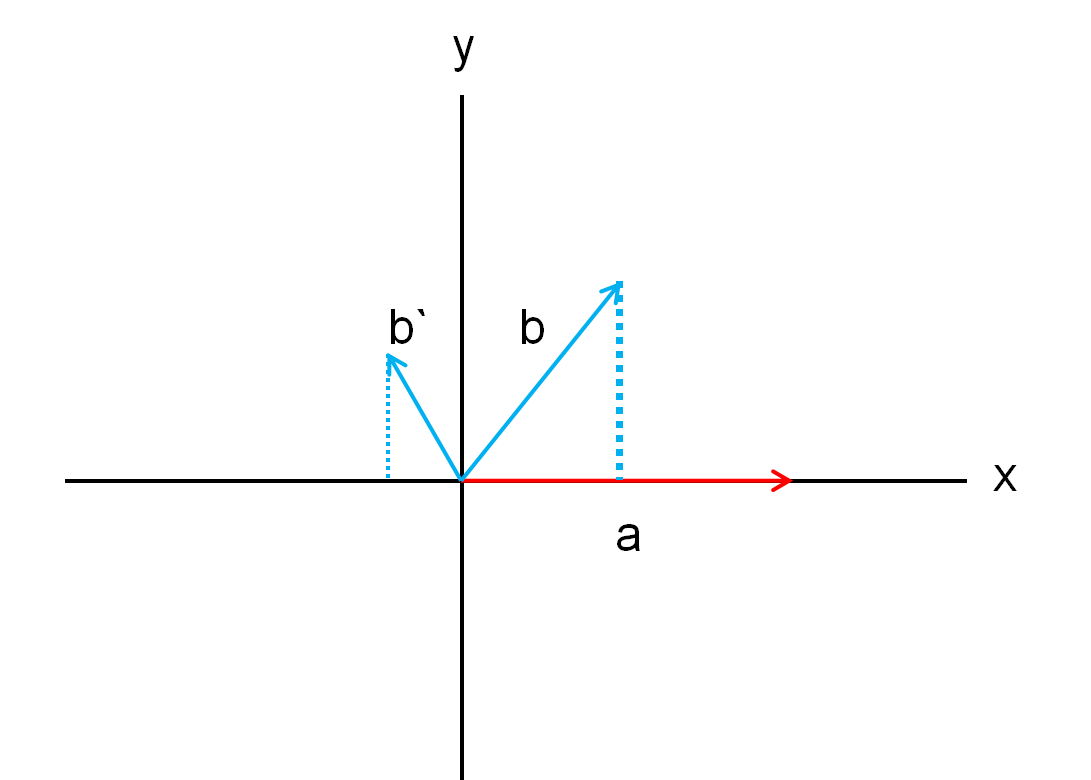

叉积

叉积的概念: 叉积的绝对值代表a,b向量围合起来的四边形的面积,正负表示两个向量相对的位置。

a,b向量的叉积 = x1*y2 - y1*x2。

叉积的绝对值代表a,b向量围合起来的四边形的面积，而正负代表后一个向量位于前一个向量的什么位置(注意这里和点积有区别，向量相乘的先后对于叉积是有影响的)。

现在a先b后，如果a位于b的顺时针方向(180度内)，那么叉积为正。反之为负，如果共线，则为0。

如下图所示,a向量与b向量的叉积为正,因为a在b的顺时针方向。而a向量与b`的向量的叉积为负。

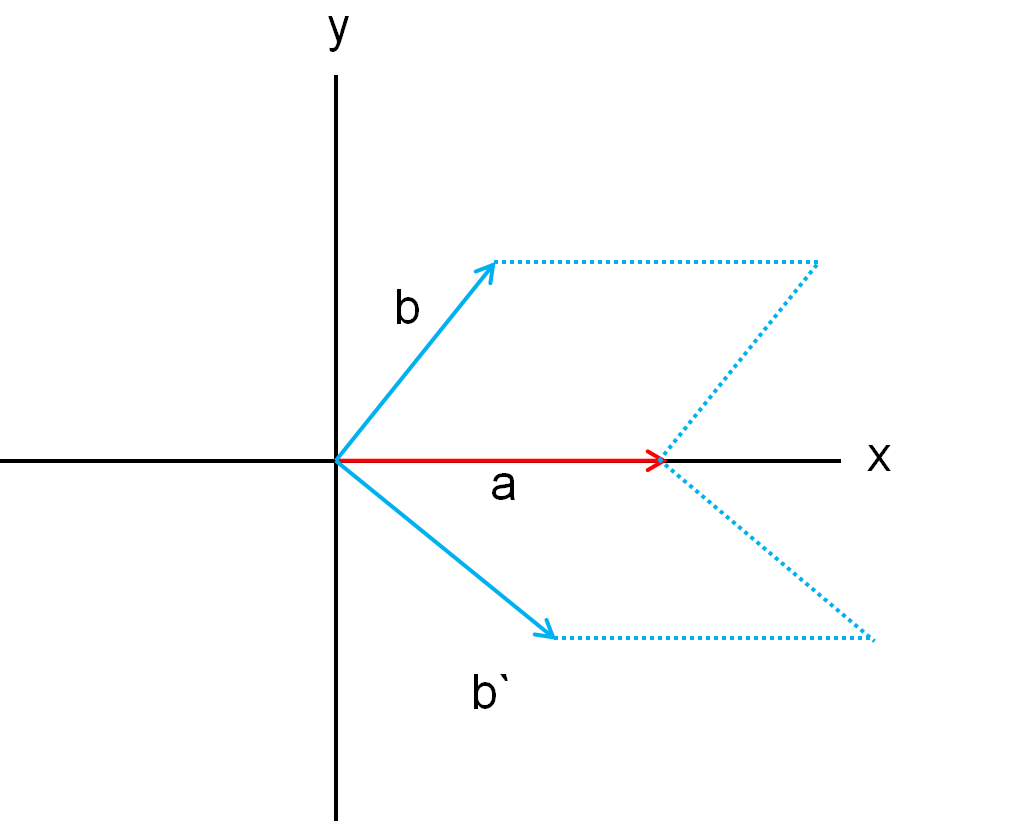
应用:判断两线段是否相交,并求交点

现在我们手中已经有了判断向量间角度大小,方位的强力工具了。下面我介绍两线段相交的例子,看看叉积与点积是如何应用的。

首先介绍一下对于点,向量的构造:

#python类实现

#点类
class Point2D():
    def __init__(self,x,y):
        self.x = x
        self.y = y
#向量类
class Vector():
    def __init__(self,x,y):
        self.x = x
        self.y = y
    def dot(self, vec):
        # 向量的点积
        return self.x*vec.x+self.y*vec.y
    def cross(self,vec):
        #向量的叉积
        return self.x*vec.y-self.y*vec.x

#线段,就不用类表示了
line1 = [point_a,point_b]
line2 = [point_0,point_1]

可以看到点和向量的构造都是由x,y构成的,向量这里我没有加起始点,所以后面的计算要根据情况给向量的起始点。线段暂且不用类表示,用两个点的列表代替,因为我觉得这样比较容易理解。

如下图所示

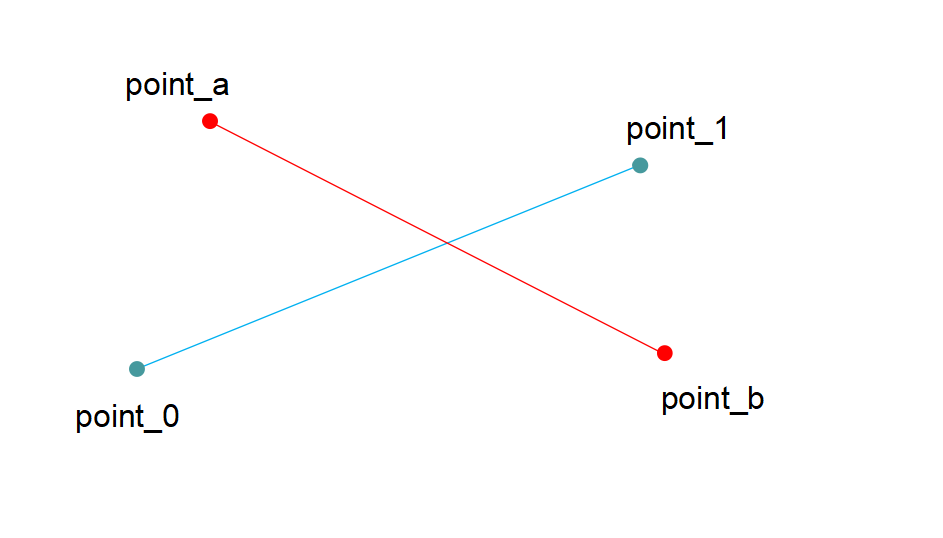
判断相交

所谓的线段相交,其实就是line1的两个点在line2的两侧并且line2的两个点在line1的两侧。

那么问题的关键就是如何判断两个点是否在一个线段的两侧。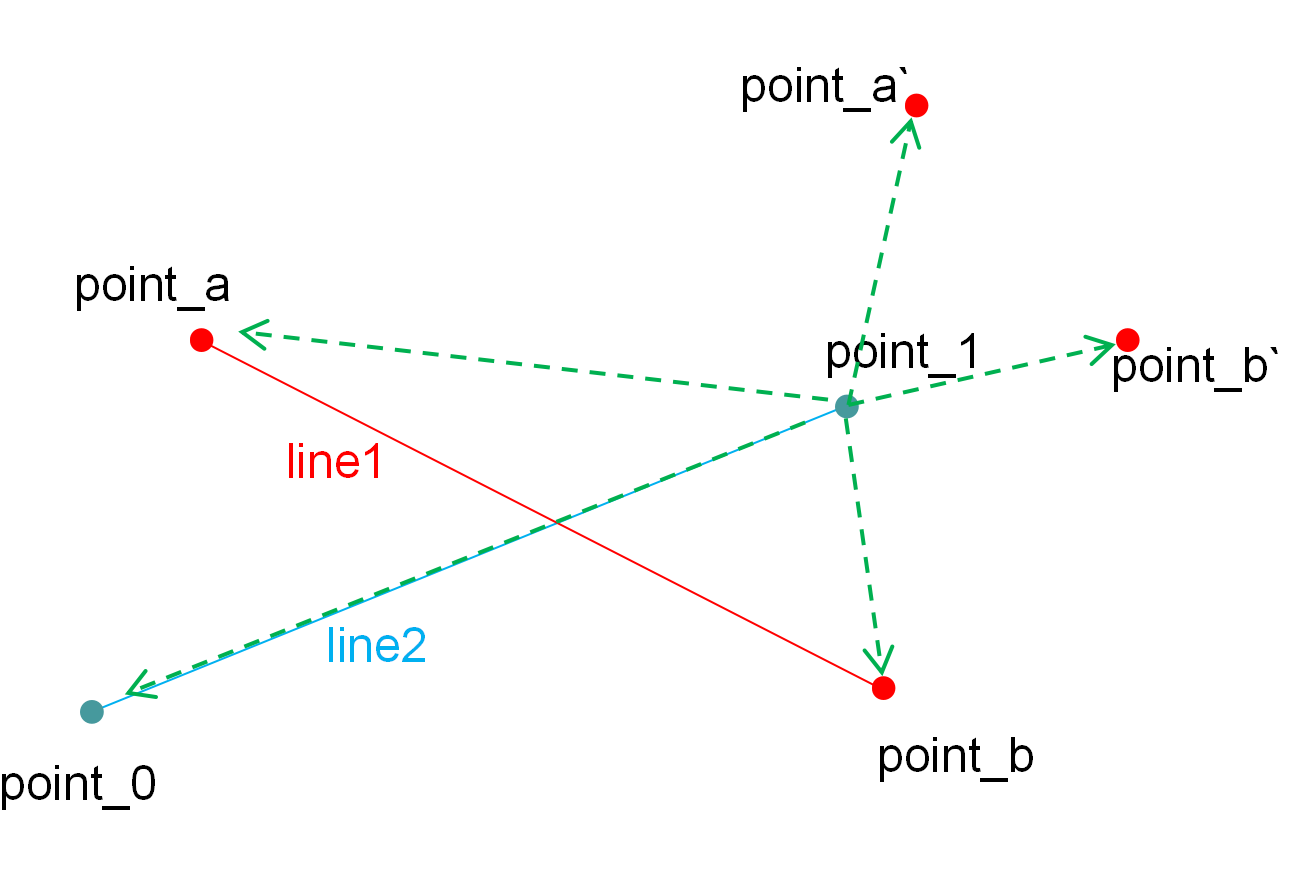

刚刚介绍的叉积就有了用武之地,看图我们可以知道line2的向量是(point_1,point_0),而点point_1到point_a的向量与点point_1到point_b的向量其实是在line2向量的两侧,而这个用叉积表示就是一个正一个负。

注意,如果是point_a变成了point_a`,point_b变成了point_b`。
那么同样会产生一正一负的结果,所以我们需要对line1也进行一次判定,当两次都成立时，我们认为这两个线段相交。

anwser = None
vector_ab = Vector(point_b.x-point_a.x,point_b.y-point_a.y)
vector_a0 = Vector(point_0.x-point_a.x,point_0.y-point_a.y)
vector_a1 = Vector(point_1.x-point_a.x,point_1.y-point_a.y)
cross_ab_a0 = vector_ab.cross(vector_a0)
cross_ab_a1 = vector_ab.cross(vector_a1)
vector_01 = Vector(point_1.x-point_0.x,point_1.y-point_0.y)
vector_0a = Vector(point_a.x-point_0.x,point_a.y-point_0.y)
vector_0b = Vector(point_b.x-point_0.x,point_b.y-point_0.y)
cross_01_0a = vector_01.cross(vector_0a)
cross_01_0b = vector_01.cross(vector_0b)

#当两个线段的结果都是一正一负的时候,判断相交
if cross_AB_A0 * cross_AB_A1 < 0 and cross_01_0A * cross_01_0B < 0:
    anwser = True
else:
    anwser = False

找到交点

我们现在已经证明了两个线段有了交点，那么接下来可以直接使用直线求交点的方法。我们知道直线的表达式有很多种，这里我们用到的是直线的参数方程。

关于直线的参数方程,大家可以去下面的网站了解:

叶大在知乎的评论

对于直线参数方程的介绍

当知道直线的起始点(x0,y0),以及向量(a,b)的时候.直线的参数方程可以直接写成

x = x0 + at

y = y0 + bt

那么现在我们分别写出两个直线的参数方程

给的点与向量如下:

point1(a,b) vector1(x1,y1)

point2(c,d) vector2(x2,y2)

参数方程如下:

直线一:
x = a + x1 * t1

y = b + y1 * t1

直线二:

x = c + x2 * t2

y = d + y2 * t2

可以知道,当交点的时候x = x,y = y,也就是得到:

a + x1 * t1 = c + x2 * t2

b + y1 * t1 = d + y2 * t2

消去t1,最后我们可以得到关于t2的解:

t2 = (c*y1 - a*y1 - d*x1 + b*x1)/(y2*x1 - x2*y1)

大家可以发现,分母就是两个向量的叉积(数学真奇妙!),暗示当两向量平行或者共线的时候无法计算。

最后将t2代入到直线二的方程中,交点的(x,y)就都得到了。

后话

向量的学习入门(线代)我推荐b站的这位up主,他讲述的是向量与几何之间的关系。生动形象。

3Blue1Brown

当然向量叉积点积还能干很多啦,下次介绍如何判断阴阳角。