向量叉积在判断阴阳角中的应用

发表于 | 分类于

向量叉积在判断阴阳角中的应用

前言

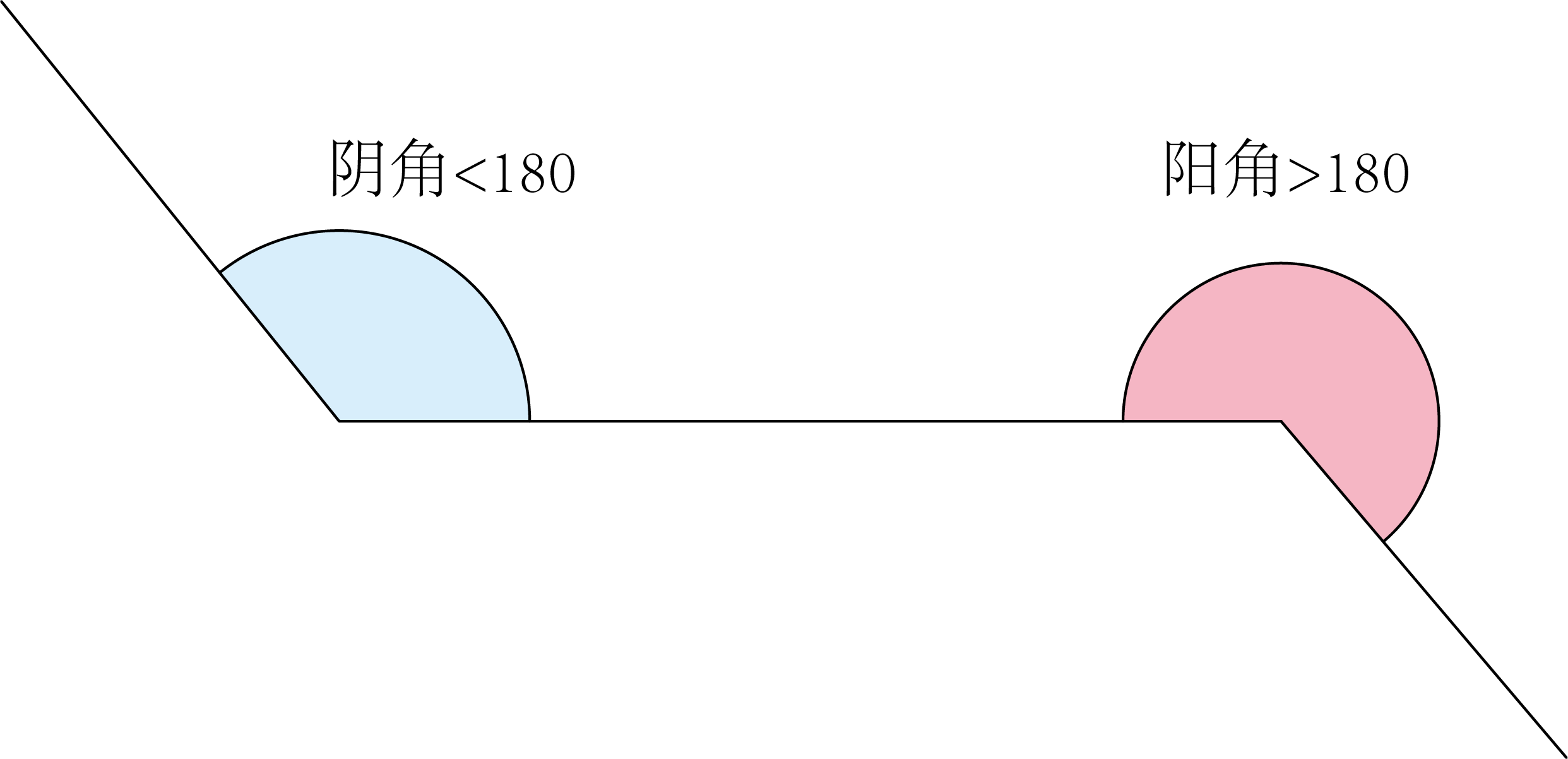
何谓阴阳角呢？

阴阳角的概念类似于凸包和凹包。在一条多段线中,相邻两条线之间所夹得角如果大于180,我们称之为阳角。反之则为阴角

阴阳角的意义？

在建筑中我们知道,如果平面中出现锐角，那么就需要注意了,因为锐角给人的仄敝的感觉,而直角和钝角就让人感觉舒适。另外包括建筑排布，光照分析，都需要知道角的性质,所以判断阴阳角是有必要的。

构造

为了判断多段线的阴阳角,我们需要构造一个多段线的类。

1
2
3
4
5
6
7
8
#python类实现

多段线类
class Polyline():
    def __init__(self,point_list):
        self.point_list = point_list

    def judge_angle(self):

我们需要给入的是一个point_list,这个列表中的元素就是我们上一次说到的point类

这个类有个判断阴阳角的函数，我们在下文会补充他

下面我把上次已经构造好的point类和vector类再发一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#python类实现

#点类
class Point2D():
    def __init__(self,x,y):
        self.x = x
        self.y = y
#向量类
class Vector():
    def __init__(self,x,y):
        self.x = x
        self.y = y
    def dot(self, vec):
        # 向量的点积
        return self.x*vec.x+self.y*vec.y
    def cross(self,vec):
        #向量的叉积
        return self.x*vec.y-self.y*vec.x

顺逆时针

有了多段线的构造,知道了阴阳角的基本概念，我们继续。

看了刚刚阴阳角的图大家是否有疑惑,其实上面应该有四个角,而我只标明了其中二个。

这就涉及到了我们到底想要让程序选择哪一面去判断。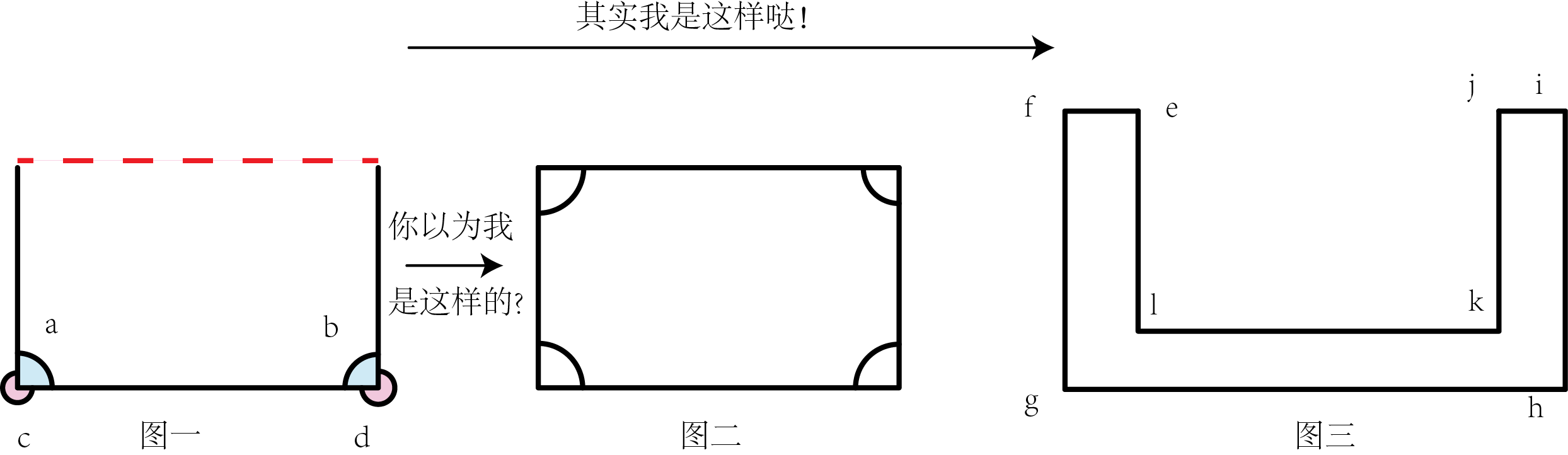

上图我们可以看到，图一可以变成图二，那么我们选择a，b两个角判断。而图一变成图三的话,我们就得判断c,d了。

选择

按照我的习惯,我会默认多段线是逆时针开始的,比如图三的闭合多段线,如果起点是e,那么这个多段线的list就是[e,f,g,h,i,j,k,l]。所以我这边默认给到的多段线是逆时针的。当然，你可以选择默认为顺时针，那么你需要注意，后面的算法中的条件需要轻微的改动。

判断

在叉积与点积的文章中我有讲到,向量a与b的叉积的正负取决于a是否在b的顺时针方向上的180内。而现在我们默认的顺序是逆时针的，所以当叉积是正的时候,代表的是大于180的情况，也就是阳角。注意，当你默认多段线是顺时针时，叉积为正代表阴角。

算法实现

现在我们实现一下上面的judge_angle函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#python类实现
#点类
class Point2D():
    def __init__(self,x,y):
        self.x = x
        self.y = y

#向量类
class Vector():
    def __init__(self,x,y):
        self.x = x
        self.y = y
    def dot(self, vec):
        # 向量的点积
        return self.x*vec.x+self.y*vec.y
    def cross(self,vec):
        #向量的叉积
 
多段线类
class Polyline():
    def __init__(self,point_list):
        self.point_list = point_list

    def judge_angle(self):
        for i in range(1,len(self.point_list)-1): #要有一个角至少三个点
            point1 = self.point_list[i-1]
            point2 = self.point_list[i]
            point3 = self.point_list[i+1]
            vector1 = Vector(point1.x-point2.x,point1.y-point2.y)
            vector2 = Vector(point3.x-point2.x,point3.y-point2.y)
            if vector1.cross(vector2) <= 0:
                print('阴角')
            else:
                print('阳角')

后话

阴阳角在很多地方都有很重要的应用。我在沿边排列中也有用到。下次有空了介绍我用来沿边排列房子的方法。