沿边排列建筑

要求

首先明确输入和输出。

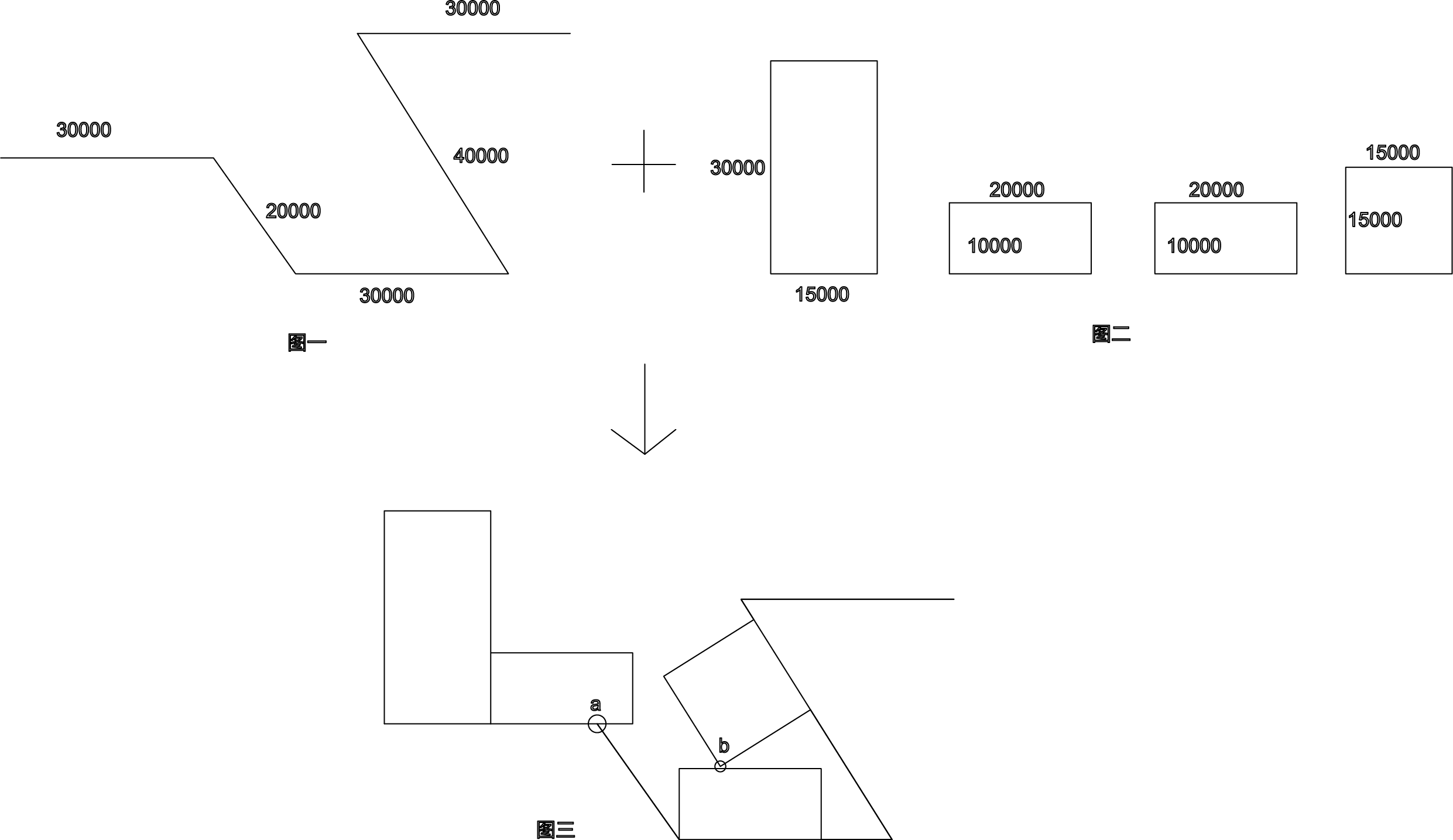
我们有图一所示的边缘线,以及图二所示的四个矩形.数据都已经在图中给出.我们要将图二的矩形在图一的边缘线上排列。

最终输入如图三所示，注意二点：

1. a处属于阳角,所以可以延伸出去。

2. b处最后一个矩形之所以这么排列，是因为前面的矩形导致的，也就是按照顺序排列。

解决方法

对于上面的问题,我采用域线的方法去解决。

我认为自己的方法只是解决这个问题的方法之一，肯定有更高效，更便捷的方法等待发现，希望我的方法能给大家一点灵感。

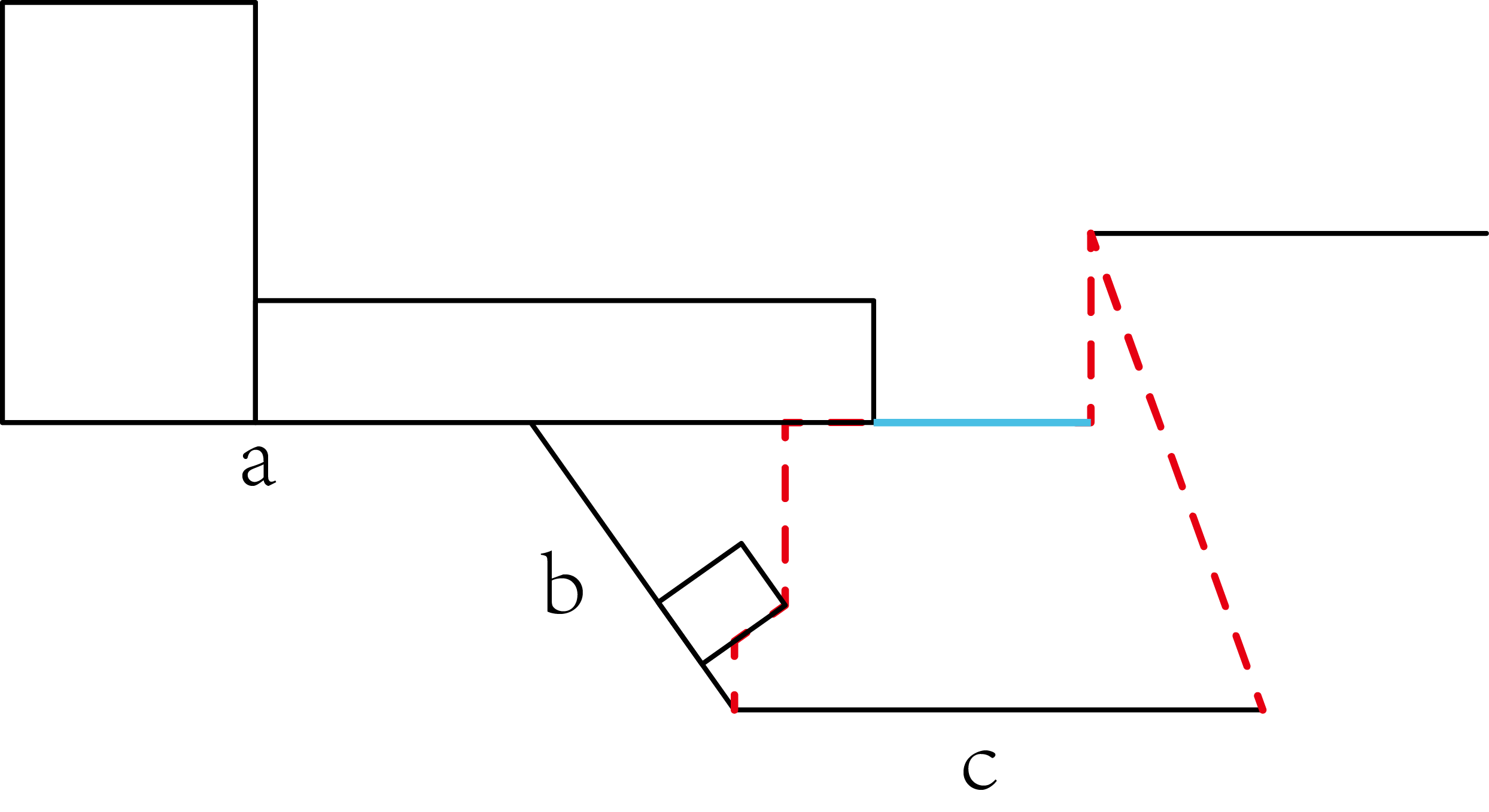
在我们已经排完a，b段后，我们现在需要排c段,那么在c段的上空可以看到,存在两条红色的域线,以及一条蓝色的中空区域(代表可以排任意高度)。得到这些域线后,就可以遍历每个域线，根据每条域线的性质来安放矩形

这就是我的大致思路。

构造

对于上述的方法需要构造几个类,分别是矩形(Rectangle),道路(Path_list),单条道路(Path),域线(Segment),域点(Areapoint).矩形与域点又继承了(Polyline),(Point2D)类.

伪代码

介绍一下具体实现的流程
可以思考一下一些具体的方法应该放在哪个类里面实现

获得域线

我们回到c段,当我们想获得c段的域线,首先得用c段之外的所有节点对c段做投影。

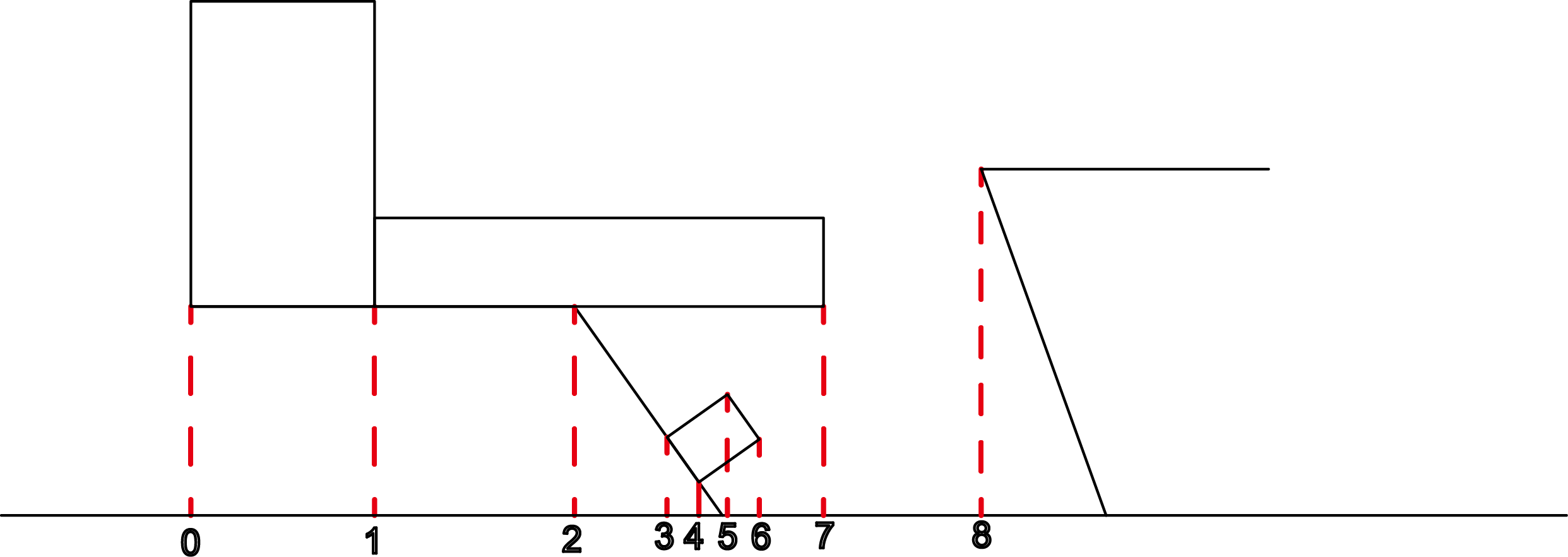
可以看到，一共9个点投影到了c段所在的直线上。

接下来对点进行一个筛选,选择5，6，7，8这几个在c段范围内的点。

然后反向将这些点与除了c段外的所有线段求垂点,并且选出最低的垂点。

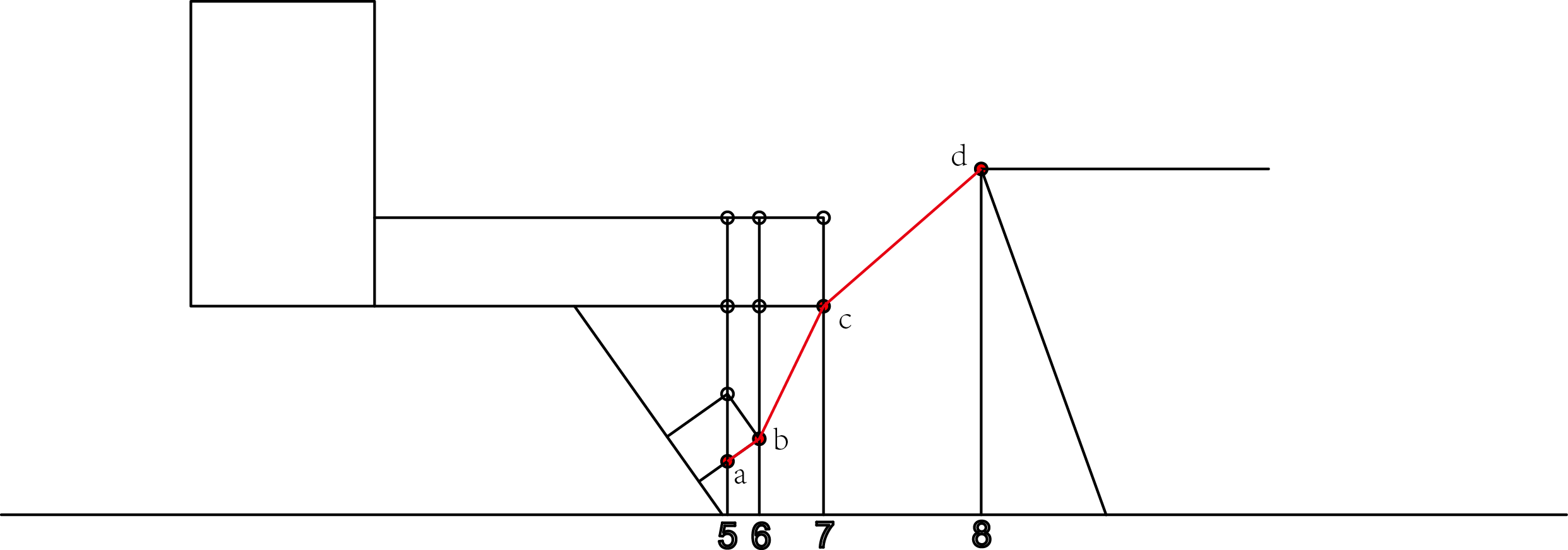
我们选出了a，b，c，d点连线。再加上c段的起始点和末尾点。在这里大家和之前主动画出来的域线比较一下会发现，b，c点间缺少一条垂直线作为过渡。

也就是说，b点其实是一个特殊的点,如何判断出b点这些特殊的点我试了一些方法，但是都没有成功…(我认为是能成功判断的，希望大家能找到方法TAT)。于是我采取了一个折中的方法，我会在每个点之间再插入若干个点，比如6，7之间再插入10个点，那么就可以得到近似于之前的域线了。由于这种方法可以用点的数量控制精度,到最后可以完美模拟,所以我认为可以采取这个方法。

还有几个应该注意的点

1/图中案例c段末尾是阴角，所以最后添加c段末端点并且把范围外的点都排除了。如果c段末尾是阳角(意味着矩形可以超出边界)，超出c段末尾的点也要被加入计算中。

2/图中c-d的域线其实是空域,所以需要一开始知道空域的范围，在算出所有域线后减去在空域中的域线

3/关于计算上的边界条件，比如遇到平行，以及除法后精确的问题

求域线的流程基本如下

#求域线的伪代码

if 阴角:
    得到除了当前段外其他所有的点
    根据角的性质排除掉不符合的点
    求空域的区间
    得到点在当前段上的投影点
    在投影点间插入精度点(按数量还是距离都随意)
    精度点反向投影到其他线段上,得到域点
    连接域点得到域线
    根据空域的区间减去空域范围的域线
    返回域线
else:
    ...

排列矩形

得到域线后就该放入矩形了,可以想象一下，我们现在要往c段放入矩形了，而c段的上方是一条条我们已经算出来的域线。而域线的种类无非三种，上升/下降/无。这里和c段平行的域线可以被看做是上升或下降的特殊情况一起讨论。下面是排列矩形的伪代码。

注意域线不存在的情况

if 阴角:
    超出c段长度结束(return)
else:
    超出c段长度加上矩形长度结束(return)

if 域线存在:
    if 域线是空值:
        看这个矩形长度范围内头上有多少域线
        判断这些域线是否与矩形相交
        if 不相交:
            可以放下，添加矩形
        else:
            移到下一个域线上
    elif 域线是上升的:
        if 域线最高点高于矩形宽:
            找到矩形切域线的位置
            看矩形长度范围内头上有多少域线
            判断这些域线是否与矩形相交
            if 不相交:
                添加矩形
            else:
                移到下一个域线上
        else:
            移到下一个域线上
    else:
        同空值
else:
    直接添加矩形

代码实现

下面我用代码实现一下，因为细节太多(包括空域其实还有种类，如何处理误差，>=之间的判断都是要反复琢磨的)，所以前面主要讲的还是逻辑,具体实现就直接上代码了。

#因为域点和矩形分别继承了Point2D和Polyline,所以我先描述这两类
#Point2D
class Point2D(object):
    def __init__(self,x,y):
        self.x = x
        self.y = y
        def addVec(self, vec):
        return Point2D([self.x + vec.x, self.y + vec.y])
    @staticmethod
    def isintersect(pointA,pointB,point0,point1):
        #判断两个线段是否有交点
        dif = 0.05 #误差
        vector_AB = Vector(pointB.x-pointA.x,pointB.y-pointA.y)
        vector_A0 = Vector(point0.x-pointA.x,point0.y-pointA.y)
        vector_A1 = Vector(point1.x-pointA.x,point1.y-pointA.y)
        cross_AB_A0 = vector_AB.cross(vector_A0)
        cross_AB_A1 = vector_AB.cross(vector_A1)
        vector_01 = Vector(point1.x-point0.x,point1.y-point0.y)
        vector_0A = Vector(pointA.x-point0.x,pointA.y-point0.y)
        vector_0B = Vector(pointB.x-point0.x,pointB.y-point0.y)
        cross_01_0A = vector_01.cross(vector_0A)
        cross_01_0B = vector_01.cross(vector_0B)
        if cross_AB_A0 * cross_AB_A1 < 0-dif and cross_01_0A * cross_01_0B < 0-dif:
            return True
        else:
            return False
    def twopointlength(self,point):
        vector = Vector(point.x-self.x,point.y-self.y)
        return vector.getLength()

#Polyline
class Polyline(object):
    def __init__(self, start_pt, vec_lst):
        self.start_pt = start_pt
        self.vec_lst = vec_lst
        self.vec_length_lst = self.getVectorLengthList()
        self.pt_lst = self.getPtListFromVectors()
        self.length = self.getLength()

    def getVectorLengthList(self):
        # 根据所有向量将长度写入矩形实例属性
        num = len(self.vec_lst)
        length_lst = [0.0]*num
        for i in range(num):
            length_lst[i] = self.vec_lst[i].length
        return length_lst
        
    def getLength(self):
        # 返回polyline的每段向量长度和
        length = 0.0
        for vec in self.vec_lst:
            length += vec.length
        return length

    def getPtListFromVectors(self):
        # 根据初始点和所有向量得到所有点, 将角点记录成向量位点
        pt_lst = []
        pt_lst.append(self.start_pt)
        temp_pt = self.start_pt
        for vec in self.vec_lst[:-1]:
            temp_pt = temp_pt.addVec(vec)
            pt_lst.append(temp_pt)
        return pt_lst

    def getVectorListFromPts(self):
        # 根据顺序点得到向量
        vec_lst = []
        for i in range(len(self.pt_lst)-1):
            vec = Vector(self.pt_lst[i], self.pt_lst[i+1])
            vec_lst.append(vec)
        vec = Vector(self.pt_lst[-1], self.pt_lst[0])
        vec_lst.append(vec)
        return vec_lst
#Vector
class Vector(object):
    def __init__(self, vec_x, vec_y, length = None):
        self.x, self.y = vec_x, vec_y
        self.length = self.getLength() if (length is None) else length
        return
    def unit(self):
        # 单位化一个向量
        return Vector(self.x/self.length, self.y/self.length, length = 1.0)

    def amplify(self, factor):
        # 向量扩大倍数
        return Vector(self.x * factor, self.y * factor, length = self.length * factor)

    def dot(self, vec):
        # 向量的点积
        return self.x*vec.x+self.y*vec.y

    def cross(self,vec):
        #向量的叉积
        return self.x*vec.y-self.y*vec.x


    def reverse(self):
        # 取反向量
        return Vector(-self.x, -self.y, length = self.length)  # 传值, 不会重新计算长度

    def rotateVertical(self):
        # 逆时针旋转90度
        return Vector(-self.y, self.x, length = self.length)


    def getLength(self):
        # 向量的长度
        return math.sqrt(self.x * self.x + self.y * self.y)


    def judgeVectorParallel(self, vec):
        # 判断实例向量和vec之间是否平行
        if self.cross(vec) == 0:
            return True
#Rectangle
 class Rectangle(Polyline):
    def ifpointin(self,point):
        #判断点是否在矩形内
        #误差
        dif = 0.05
        point_origin = self.pt_lst[0]
        point_1 = self.pt_lst[1]
        point_2 = self.pt_lst[3]
        vector_1 = Vector(point_1.x-point_origin.x,point_1.y-point_origin.y)
        vector_2 = Vector(point_2.x-point_origin.x,point_2.y-point_origin.y)
        vector = Vector(point.x-point_origin.x,point.y-point_origin.y)
        dot_1 = vector.dot(vector_1)
        dot_2 = vector.dot(vector_2)
        if dot_1 < vector_1.getLength()*vector_1.getLength()-dif and dot_1 > 0+dif and dot_2 < vector_2.getLength()*vector_2.getLength()-dif and dot_2 > 0+dif:
            return True
        else:
            return False
    def ifintersectline(self,point0,point1):
        #判断矩形是否与线段碰撞
        for i in range(0,len(self.pt_lst)-1):
            point_re_A = self.pt_lst[i]
            point_re_B = self.pt_lst[i+1]
            flag = Point2D.isintersect(point_re_A,point_re_B,point0,point1)
            #输出True代表有碰撞
            if flag == True:
                return True
        return False    
#Areapoint
class Areapoint(Point2D):
    '构造path上的域点,想要的属性有length和height'
    def __init__(self,point,path):
        self.x = point.x
        self.y = point.y
        self.hight, self.length = path.Getvertical(path.start_pt,path.vector,point)
        self.block = False
#Path
class Path():
    '构造沿边排房子的单条路'
    def __init__(self,start_x,start_y,end_x,end_y):
        self.start_pt = Point2D([start_x,start_y])
        self.end_pt = Point2D([end_x,end_y])
        self.length = self.start_pt.twopointlength(self.end_pt)
        self.vector = Vector(end_x-start_x,end_y-start_y).unit()
        self.rectangle_list = []
        self.pathpoint_list = []
        self.getreclength = 0
        self.arealist = []
        self.segmentlist = [] #用segment管理域点
        self.block_length = [-1,-1]
        self.angleclass = -1 #path的阴阳角，默认为阴角
    #切割域点
    def Cutareapoint(self,areapoint1,areapoint2,block_length):
        vector = Vector(areapoint2.x-areapoint1.x,areapoint2.y-areapoint1.y)
        area_hight = areapoint2.hight-areapoint1.hight
        area_length = areapoint2.length-areapoint1.length
        length = block_length - areapoint1.length
        k = length/area_length
        hight = areapoint1.hight + area_hight*k
        vector = vector.amplify(k)
        temp_point = areapoint1.addVec(vector)
        anwser = copy.copy(areapoint1)
        anwser.x = temp_point.x
        anwser.y = temp_point.y
        anwser.hight = hight
        anwser.length = block_length
        return anwser
    #根据域点得到域线
    def Getsegmentlist(self):
        '''策略是用空域的值分割域线'''
        temp_list = []
        for i in range(0,len(self.arealist)-1):
            point_0 = self.arealist[i]
            point_1 = self.arealist[i+1]
            segment_list = []
            if point_0.length < self.block_length[0]:
                #当segment的第一个点在区间的左侧
                if point_1.length <= self.block_length[0]:
                    segment_list.append(Segment(point_0,point_1))
                elif point_1.length <= self.block_length[1]:
                    segment_list.append(Segment(point_0,self.Cutareapoint(point_0,point_1,self.block_length[0])))
                else:
                    segment_list.append(Segment(point_0,self.Cutareapoint(point_0,point_1,self.block_length[0])))
                    segment_list.append(Segment(self.Cutareapoint(point_0,point_1,self.block_length[1]),point_1))
            elif point_0.length == self.block_length[0]:
                if point_1.length <= self.block_length[1]:
                    None
                else:
                    segment_list.append(Segment(self.Cutareapoint(point_0,point_1,self.block_length[1]),point_1))
            elif point_0.length < self.block_length[1]:
                #当segment的第一个点在区间内，有二种情况
                if point_1.length <= self.block_length[1]:
                    None
                else:
                    segment_list.append(Segment(self.Cutareapoint(point_0,point_1,self.block_length[1]),point_1))
            else:
                segment_list.append(Segment(point_0,point_1))
            if segment_list != []:
                for i in segment_list:
                    segmentclass = self.Isareaclass(i.start_pt,i.end_pt)
                    i.updownclass = segmentclass
                    temp_list.append(i)
        self.segmentlist = temp_list

    #根据getreclength与segment确认当前getreclangth对应的segment
    def Getnowsegment(self):
        #先找到老的getreclength位于什么segment
        #判断的根据是getreclength大于等于segment的起始length,小于末尾的length
        for i in range(0,len(self.segmentlist)):
            if self.getreclength >= self.segmentlist[i].start_pt.length and self.getreclength < self.segmentlist[i].end_pt.length:
                return self.segmentlist[i]
        return False 
    #根据getreclength与矩形的length确认经过多少的segment
    def Findsegmentnumber(self,length):
        '''判断标准是segment是否有点在区间内或者区间点是否在segment'''
        segment_list = []
        st_length = self.getreclength
        end_length = self.getreclength + length
        for i in self.segmentlist:
            seg_st_length = i.start_pt.length
            seg_end_length = i.end_pt.length
            flag = 0
            if st_length<=seg_st_length and end_length >= seg_st_length:
                flag = 1
            if st_length<=seg_end_length and end_length >= seg_end_length:
                flag = 1
            if seg_st_length<=st_length and seg_end_length >= st_length:
                flag = 1
            if seg_st_length<=end_length and seg_end_length >= end_length:
                flag = 1
            if flag == 1:
                segment_list.append(i)
        return segment_list
    #得到一个矩形和一组segment
    def Selectsegment(self,segment_list,rec):
        for i in segment_list:
            point0 = i.start_pt
            point1 = i.end_pt
            tuch_0 = rec.ifpointin(point0)
            tuch_1 = rec.ifpointin(point1)
            if rec.ifintersectline(point0,point1) == True or tuch_0 == True or tuch_1 == True: #如果有碰撞
                return False #则不行
        return True #如果一圈下来都没有碰撞,那么返回True
            
    #给予距离start_point的距离,矩形的长宽,得到该矩形
    def PathaddRectangle(self,distance,length,weight):
        length_vector = self.vector.amplify(distance)
        start_point = Point2D([self.start_pt.x+length_vector.x,self.start_pt.y+length_vector.y])
        #矩形的宽方向上向量
        vec_x = Vector(-1*self.vector.y,self.vector.x)
        vec_x = vec_x.amplify(weight)
        #矩形的长方向上向量
        vec_y = Vector(self.vector.x,self.vector.y)
        vec_y = vec_y.amplify(length)
        #得到负的x,y向量
        vec_x_na = vec_x.reverse()
        vec_y_na = vec_y.reverse()
        vec_lst = [vec_x,vec_y,vec_x_na,vec_y_na] #得到矩形所需的向量列表
        temp_rec = Rectangle(start_point,vec_lst) #得到矩形
        return temp_rec

    #得到一条该path上的边缘线(点列表),从start_pt开始
    def Getpath(self):
        self.pathpoint_list.append(self.start_pt)
        for i in self.rectangle_list:
            for z in i.pt_lst:
                self.pathpoint_list.append(z)
        self.pathpoint_list.append(self.end_pt)
        temp_list = self.pathpoint_list
        return temp_list
    #得到该path上所有的点
    def Getpoint(self):
        point_list = []
        point_list.append(self.start_pt)
        for i in self.rectangle_list:
            for z in i.pt_lst:
                point_list.append(z)
        point_list.append(self.end_pt)
        return point_list
    #得到该path上所有的segment
    def Getsegment(self):
        segment_list = []
        segment_list.append(Segment(self.start_pt,self.end_pt))
        for i in self.rectangle_list:
            for z in range(0,len(i.pt_lst)):
                temp_segment = Segment(i.pt_lst[z],i.pt_lst[(z+1)%4])
                segment_list.append(temp_segment)
        return segment_list

    #给一个向量和向量起点,返回点到点在向量垂点上的距离与起始点和垂点的length
    def Getvertical(self,st_point,vector,point):
        point_vector = Vector(vector.y*(-1),vector.x)
        vertical_point = PointVec.rayrayIntersect(st_point,vector,point,point_vector)
        height = vertical_point.twopointlength(point)
        length = vertical_point.twopointlength(st_point)
        return height, length

    #得到碰到上升域线的点
    def Getrasepoint(self,st_point,end_point,weight):
        st_end_hight_dif = end_point.hight - st_point.hight #高度差
        st_end_length_dif = end_point.length - st_point.length #距离差
        #print('st_end = ',st_end_hight_dif,st_end_length_dif)
        if st_end_hight_dif == 0:
            return st_point
        elif weight <= st_point.hight:
            return st_point
        else:
            anwser_point = st_point
            dif = (weight-st_point.hight)/st_end_hight_dif
            st_end_x_dif = end_point.x - st_point.x
            st_end_y_dif = end_point.y - st_point.y
            anwser_point.x += st_end_x_dif*dif
            anwser_point.y += st_end_y_dif*dif
            anwser_point.hight += st_end_hight_dif*dif
            anwser_point.length += st_end_length_dif*dif
            return anwser_point
    #给两个域线上的点,返回这两个点的类型
    def Isareaclass(self,st_point,end_point):
        '''一共三种类型，上升/中空/下降，对应0/1/2'''
        st_length = self.vector.dot(Vector(st_point.x-self.start_pt.x,st_point.y-self.start_pt.y))
        end_length = self.vector.dot(Vector(end_point.x-self.start_pt.x,end_point.y-self.start_pt.y))
        temp_vector = Vector(end_point.x-st_point.x,end_point.y-st_point.y)
        cross_value = self.vector.cross(temp_vector)
        #print('st_length',st_length,'end_length',end_length,'block',self.block_length[0])
        #if st_length >= self.block_length[0] and st_length <= self.block_length[1]+0.5 and end_length >= self.block_length[0] and end_length <= self.block_length[1]+0.5:
        #    return 1
        if cross_value >= 0:
            return 0
        else:
            return 2

 
    #排一个矩形
    def Intersectrec(self,weight,length):
        #如果是阴角的情况getreclenght超出了path的长度
        if self.angleclass == -1:
            if self.getreclength+length > self.length:
                return False
        else:
            if self.getreclength >= self.length:
                return False
        #首先讨论域线存在的情况
        if self.segmentlist != []:
            segment = self.Getnowsegment()
            #中空的情况
            if segment == False:
                '''不存在装不下的情况,也不用去找tuchpoint,直接用原始的getreclength计算'''
                segment_list = self.Findsegmentnumber(length)
                rec = self.PathaddRectangle(self.getreclength,length,weight)
                flag = self.Selectsegment(segment_list,rec)
                if flag == True:
                    '''成功'''
                    self.rectangle_list.append(rec)
                    self.getreclength += length
                    return True
                else:
                    self.getreclength = segment_list[0].start_pt.length #中空无seg,所以用seg列表中的代替
                    return self.Intersectrec(weight,length)
            #上升的情况
            elif segment.updownclass == 0: 
                max_hight = segment.end_pt.hight
                if max_hight < weight: #如果最高点都装不下
                    '''移动getreclength,递归函数'''
                    self.getreclength = segment.end_pt.length
                    return self.Intersectrec(weight,length)
                else: #如果最高点装的下的情况
                    '''更新getreclength,并且算出经过几个域点'''
                    #如果没碰到,则按照原样
                    if weight > segment.start_pt.hight:
                        tuch_point = self.Getrasepoint(segment.start_pt,segment.end_pt,weight)
                        self.getreclength = tuch_point.length
                    segment_list = self.Findsegmentnumber(length)
                    rec = self.PathaddRectangle(self.getreclength,length,weight)
                    flag = self.Selectsegment(segment_list,rec)
                    if flag == True:
                        '''没有碰到,成功了'''
                        self.rectangle_list.append(rec) #将矩形加入path
                        self.getreclength += length
                        return True
                    else:
                        '''有碰到，说明这条不行,跳到末点'''
                        self.getreclength = segment.end_pt.length
                        return self.Intersectrec(weight,length) #递归函数
            #下降的情况
            else:
                '''下降也是直接用原始的getreclength计算即可'''
                segment_list = self.Findsegmentnumber(length)
                rec = self.PathaddRectangle(self.getreclength,length,weight)
                flag = self.Selectsegment(segment_list,rec)
                if flag == True:
                    '''成功'''
                    self.rectangle_list.append(rec)
                    self.getreclength += length
                    return True
                else:
                    self.getreclength = segment.end_pt.length
                    return self.Intersectrec(weight,length)
        #域线不存在的时候
        else:
            '''直接得到rec,更新getreclength'''
            rec = self.PathaddRectangle(self.getreclength,length,weight)
            self.rectangle_list.append(rec)
            self.getreclength += length
            return True
#Path_list
class Path_list():
    '构造沿边排房子单条路的集合'
    #接受point2D的集合
    def __init__(self,point_list):
        self.point_list = point_list
        self.close = False #是否闭合
        self.path_number = len(point_list)-1
        self.path_list = [] #储存path
        if self.point_list[0].x == self.point_list[-1].x and self.point_list[0].y == self.point_list[-1].y:
            self.close = True
        #初始化path_list
        for i in range(0,len(point_list)-1):
            path = Path(point_list[i].x,point_list[i].y,point_list[i+1].x,point_list[i+1].y)
            self.path_list.append(path)
    #得到每个path的阴阳角判定
    def Getangleclass(self):
        if len(self.path_list) > 1:
            for i in range(0,len(self.path_list)-1):
                path1 = self.path_list[i]
                path2 = self.path_list[i+1]
                vector1 = Vector(path1.end_pt.x-path1.start_pt.x,path1.end_pt.y-path1.start_pt.y)
                vector2 = Vector(path2.end_pt.x-path2.start_pt.x,path2.end_pt.y-path2.start_pt.y)
                vector1_ver = Vector(vector1.y*-1,vector1.x)
                if vector2.dot(vector1_ver) > 0:
                    self.path_list[i].angleclass = -1 #为阴角
                else:
                    self.path_list[i].angleclass = 1 #为阳角

    #返回边界
    def Getsize(self):
        anwser_list = []
        for i in self.path_list:
            temp_list = i.Getpath()
            temp_list = temp_list[:-1]
            for z in temp_list:
                anwser_list.append(z)
        anwser_list.append(self.path_list[-1].Getpath()[-1])
        return anwser_list
    #得到普通点列表,转化为域点
    def Getareapointlist(self,point_list,path):
        temp_list = []
        for i in point_list:
            areapoint = Areapoint(i,path)
            temp_list.append(areapoint)
        path.arealist = temp_list
    #排矩形,得到一组长宽的列表
    def Arrangerec(self,recmessage):
        '''迭代path的列表，能排就排，不能排就换下一条'''
        path_number = len(self.path_list)
        cnt = 0
        for i in range(0,int(len(recmessage)/2)):
            for z in range(cnt,len(self.path_list)):
                self.Getarea(z)
                anwser = self.path_list[z].Intersectrec(recmessage[i*2],recmessage[i*2+1])
                if anwser == True:
                    break
                else:
                    cnt += 1
    #返回index两边的边界(pint_list)      
    def Gettwosize(self,index):
        small_list = [self.path_list[index].start_pt]
        big_list = [self.path_list[index].end_pt]
        #得到小于index的一边
        for i in range(0,index):
            temp = index-i-1
            temp_list = self.path_list[temp].Getpath()
            temp_list.reverse()
            temp_list = temp_list[1:]
            for z in temp_list:
                small_list.append(z)
        #得到大于index的一边
        for i in range(index+1,self.path_number):
            temp = i
            temp_list = self.path_list[temp].Getpath()
            temp_list = temp_list[1:]
            for z in temp_list:
                big_list.append(z)
        return small_list,big_list
    #返回除了index外的点
    def Getotherpoint(self,index):
        point_list = []
        small_list = []
        big_list = []
        for i in range(0,index):
            temp_small = self.path_list[i].Getpoint()
            for z in temp_small:
                small_list.append(z)
        for i in range(index+1,self.path_number):
            temp_big = self.path_list[i].Getpoint()
            for z in temp_big:
                big_list.append(z)
        for i in range(0,len(self.path_list)):
            if i != index:
                temp_point_list = self.path_list[i].Getpoint()
                for z in temp_point_list:
                    point_list.append(z)
        return point_list, small_list, big_list
    #返回除了index外的segment
    def Getotherseg(self,index):
        segment_list = []
        for i in range(0,len(self.path_list)):
            if i != index:
                temp_segment_list = self.path_list[i].Getsegment()
                for z in temp_segment_list:
                    segment_list.append(z)
        return segment_list
    #判断一个点是否在index线的上空
    def isFlay(self,index,point):
        path = self.path_list[index]
        path_vector = path.vector
        path_vector.na = path_vector.reverse()
        path_start_vector = Vector(point.x-path.start_pt.x,point.y-path.start_pt.y)
        path_end_vector = Vector(point.x-path.end_pt.x,point.y-path.end_pt.y)
        if path_vector.dot(path_start_vector) >= 0 and path_vector.cross(path_start_vector) >= 0 and path_vector.na.dot(path_end_vector) >= 0 and path_vector.na.cross(path_end_vector) <= 0:
            return True
        else:
            return False
    #判断阳角上的域点
    def isFlay1(self,index,point):
        path = self.path_list[index]
        path_vector = path.vector
        path_vector.na = path_vector.reverse()
        path_start_vector = Vector(point.x-path.start_pt.x,point.y-path.start_pt.y)
        path_end_vector = Vector(point.x-path.end_pt.x,point.y-path.end_pt.y)
        if path_vector.dot(path_start_vector) >= 0 and path_vector.cross(path_start_vector) > 0:  #and path_vector.na.dot(path_end_vector) >= 0 and path_vector.na.cross(path_end_vector) <= 0
            return True
        else:
            return False
    #判断中空点
    def isFlaytwo(self,index,point):
        path = self.path_list[index]
        path_vector = path.vector
        path_vector.na = path_vector.reverse()
        path_start_vector = Vector(point.x-path.start_pt.x,point.y-path.start_pt.y)
        path_end_vector = Vector(point.x-path.end_pt.x,point.y-path.end_pt.y)
        if path_vector.cross(path_start_vector) >= 0:
            return True
        else:
            return False
    #返回点在线上的长度
    def Getlength(self,index,point_list):
        vector_length = []
        index_start_pt = self.path_list[index].start_pt
        index_end_pt = self.path_list[index].end_pt
        index_vector = self.path_list[index].vector
        index_vector_unit = index_vector.unit()
        for i in point_list:
            temp_vector = Vector(i.x-index_start_pt.x,i.y-index_start_pt.y)
            temp_length = index_vector_unit.dot(temp_vector)
            vector_length.append(temp_length)
        return vector_length
    #返回一条域线
    def Getarea(self,index):
        #分别讨论域线阴阳角的区别
        #当是阴角的情况(小于180)
        if self.path_list[index].angleclass == -1: 
            all_point,small_point,big_point = self.Getotherpoint(index)
            all_segment = self.Getotherseg(index)
            vector_length = []
            index_vector = self.path_list[index].vector
            interset_vector = Vector(-1*index_vector.y,index_vector.x)
            index_start_pt = self.path_list[index].start_pt
            index_end_pt = self.path_list[index].end_pt
            anwser_list = [index_start_pt]
            #求中空区间的length
            block_length = []
            small_point_temp = []
            big_point_temp = []
            for i in small_point:
                if self.isFlaytwo(index,i):
                    small_point_temp.append(i)
            for i in big_point:
                if self.isFlaytwo(index,i):
                    big_point_temp.append(i)
            small_point = small_point_temp
            big_point = big_point_temp
            small_length = self.Getlength(index,small_point)
            big_length = self.Getlength(index,big_point)
            small_length.sort()
            big_length.sort()

            if small_length != [] and big_length != []:
                if small_length[-1] < big_length[0]:
                    block_length = [small_length[-1],big_length[0]]
                else:
                    block_length = [-1,-1]
            elif small_length == [] and big_length == []:
                block_length = [0,self.path_list[index].length]
            elif small_length == [] and big_length[0] > 0:
                block_length = [0,big_length[0]]
            elif big_length == [] and small_length[-1] < self.path_list[index].length:
                block_length = [small_length[-1],self.path_list[index].length]
            else:
                block_length = [-1,-1]
            #
            index_vector_unit = index_vector.unit()
            #求length_vector
            vector_length = self.Getlength(index,all_point)
            temp_vector_length = []
            ###精度
            diff = 10
            for i in range(0,len(vector_length)):
                if vector_length[i] > 0 and vector_length[i] < self.path_list[index].length:
                    temp_vector_length.append(vector_length[i])
            vector_length = list(set(temp_vector_length))
            vector_length.sort()
            if vector_length != []:
                st_value = vector_length[0]/diff
                end_value = (self.path_list[index].length-vector_length[-1])/diff
                temp_vector_length = []
                for i in range(1,diff-1):
                    temp_vector_length.append(i*st_value)
                for i in range(0,len(vector_length)-1):
                    temp_vector_length.append(vector_length[i])
                    value = (vector_length[i+1]-vector_length[i])/diff
                    for z in range(1,diff-1):
                        temp_vector_length.append(vector_length[i]+z*value)
                temp_vector_length.append(vector_length[-1])
                vector_length = temp_vector_length
            ###插入其他点
            difff = 1000
            temp_value = difff
            while(temp_value<self.path_list[index].length):
                vector_length.append(temp_value)
                temp_value += difff
            vector_length = list(set(vector_length))
            vector_length.sort()
            #
            for i in vector_length:
                temp_point = index_start_pt.addVec(index_vector_unit.amplify(i))
                temp_inter_list = []
                now_inter_list = []
                for z in all_segment:
                    temp_anwser = z.interpoint(temp_point,interset_vector)
                    if temp_anwser[0] == True:
                        temp_inter_list.append(temp_anwser[1])
                for i in range(0,len(temp_inter_list)):
                    if self.isFlay(index,temp_inter_list[i]) == True:
                        now_inter_list.append(temp_inter_list[i])
                temp_inter_list = now_inter_list
                if temp_inter_list == []:
                    None
                else:
                    min = 11111111
                    anwser_point = temp_inter_list[0]
                    for q in temp_inter_list:
                        length = q.twopointlength(temp_point)
                        if length <= min:
                            min = length
                            anwser_point = q
                    anwser_list.append(anwser_point)
            anwser_list.append(index_end_pt)
            self.Getareapointlist(anwser_list,self.path_list[index])
            self.path_list[index].block_length = block_length
            self.path_list[index].Getsegmentlist() #得到域线
            return anwser_list, block_length
        else:
            all_point,small_point,big_point = self.Getotherpoint(index)
            all_segment = self.Getotherseg(index)
            vector_length = []
            index_vector = self.path_list[index].vector
            interset_vector = Vector(-1*index_vector.y,index_vector.x)
            index_start_pt = self.path_list[index].start_pt
            index_end_pt = self.path_list[index].end_pt
            anwser_list = [index_start_pt]
            #求中空区间的length
            block_length = []
            small_point_temp = []
            big_point_temp = []
            for i in small_point:
                if self.isFlaytwo(index,i):
                    small_point_temp.append(i)
            for i in big_point:
                if self.isFlaytwo(index,i):
                    big_point_temp.append(i)
            small_point = small_point_temp
            big_point = big_point_temp
            small_length = self.Getlength(index,small_point)
            big_length = self.Getlength(index,big_point)
            small_length.sort()
            big_length.sort()

            if small_length != [] and big_length != []:
                if small_length[-1] < big_length[0]:
                    block_length = [small_length[-1],big_length[0]]
                else:
                    block_length = [-1,-1]
            elif small_length == [] and big_length == []:
                block_length = [0,self.path_list[index].length]
            elif small_length == [] and big_length[0] > 0:
                block_length = [0,big_length[0]]
            elif big_length == [] and small_length[-1] < self.path_list[index].length:
                block_length = [small_length[-1],self.path_list[index].length]
            else:
                block_length = [-1,-1]
            #
            index_vector_unit = index_vector.unit()
            #求length_vector
            vector_length = self.Getlength(index,all_point)
            temp_vector_length = []
            ###精度
            diff = 10
            for i in range(0,len(vector_length)):
                if vector_length[i] > 0: # and vector_length[i] < self.path_list[index].length
                    temp_vector_length.append(vector_length[i])
            vector_length = list(set(temp_vector_length))
            vector_length.sort()
            if vector_length != []:
                st_value = vector_length[0]/diff
                end_value = (self.path_list[index].length-vector_length[-1])/diff
                temp_vector_length = []
                for i in range(1,diff-1):
                    temp_vector_length.append(i*st_value)
                for i in range(0,len(vector_length)-1):
                    temp_vector_length.append(vector_length[i])
                    value = (vector_length[i+1]-vector_length[i])/diff
                    for z in range(1,diff-1):
                        temp_vector_length.append(vector_length[i]+z*value)
                temp_vector_length.append(vector_length[-1])
                vector_length = temp_vector_length
            ###插入其他点
            difff = 1000
            temp_value = difff
            while(temp_value<self.path_list[index].length):
                vector_length.append(temp_value)
                temp_value += difff
            vector_length = list(set(vector_length))
            vector_length.sort()
            #
            for i in vector_length:
                temp_point = index_start_pt.addVec(index_vector_unit.amplify(i))
                temp_inter_list = []
                now_inter_list = []
                for z in all_segment:
                    temp_anwser = z.interpoint(temp_point,interset_vector)
                    if temp_anwser[0] == True:
                        temp_inter_list.append(temp_anwser[1])
                for i in range(0,len(temp_inter_list)):
                    if self.isFlay1(index,temp_inter_list[i]) == True:
                        now_inter_list.append(temp_inter_list[i])
                temp_inter_list = now_inter_list
                if temp_inter_list == []:
                    None
                else:
                    min = 11111111
                    anwser_point = temp_inter_list[0]
                    for q in temp_inter_list:
                        length = q.twopointlength(temp_point)
                        if length <= min and length != 0:
                            min = length
                            anwser_point = q
                    anwser_list.append(anwser_point)
            self.Getareapointlist(anwser_list,self.path_list[index])
            self.path_list[index].block_length = block_length
            self.path_list[index].Getsegmentlist() #得到域线
            return anwser_list, block_length
 
#Segment
class Segment():
    def __init__(self,start_pt,end_pt):
        self.vector = Vector(end_pt.x-start_pt.x,end_pt.y-start_pt.y)
        self.start_pt = start_pt
        self.end_pt = end_pt
        self.updownclass = 0 #0上升1下降
    #给一条射线,判断是否有交点,如果平行输出最近的点
    def interpoint(self,point,vector):
        if self.vector.judgeVectorParallel(vector):
            st_vector = Vector(self.start_pt.x-point.x,self.start_pt.y-point.y)
            if st_vector.cross(vector) == 0:
                st_length = self.start_pt.twopointlength(point)
                end_length = self.end_pt.twopointlength(point)
                if st_length > end_length:
                    return [True,self.start_pt]
                else:
                    return [True,self.end_pt]
            else:
                return [False]
        else:
            temp_point = PointVec.rayrayIntersect(self.start_pt,self.vector,point,vector)
            temp_point_vector = Vector(temp_point.x-self.start_pt.x,temp_point.y-self.start_pt.y)
            dotlin_lin = self.vector.dot(self.vector)
            dotlin_ver = self.vector.dot(temp_point_vector)
            if dotlin_ver < 0+(-0.5) or dotlin_ver > dotlin_lin+0.5:
                return [False]
            else:
                return [True,temp_point]

好吧好吧，实在是有点长。很多精力都花费在了边界条件上，比如一个大于等于0会造成什么后果,如何处理这种问题还得多总结。